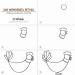
Uhol ABC je vpísaný uhol. Opiera sa o oblúk AC, uzavretý medzi jeho stranami (obr. 330).
Veta. Vpísaný uhol sa meria polovicou oblúka, na ktorom sa nachádza.
Toto by sa malo chápať takto: vpísaný uhol obsahuje toľko uhlových stupňov, minút a sekúnd, koľko je oblúkových stupňov, minút a sekúnd obsiahnutých v polovici oblúka, na ktorom spočíva.
Pri dokazovaní tejto vety je potrebné zvážiť tri prípady.
Prvý prípad. Stred kružnice leží na strane vpísaného uhla (obr. 331).
Nech ∠ABC je vpísaný uhol a stred kružnice O leží na strane BC. Je potrebné preukázať, že sa meria pol oblúka AC.
Spojme bod A so stredom kruhu. Získame rovnoramenný \(\Delta\)AOB, v ktorom AO = OB, ako polomery tej istej kružnice. Preto ∠A = ∠B.
∠AOC je vonkajší trojuholník AOB, takže ∠AOC = ∠A + ∠B, a keďže uhly A a B sú rovnaké, potom ∠B je 1/2 ∠AOC.
Ale ∠AOC sa meria oblúkom AC, preto ∠B sa meria polovicou oblúka AC.
Napríklad, ak \(\breve(AC)\) obsahuje 60°18', potom ∠B obsahuje 30°9'.
Druhý prípad. Stred kružnice leží medzi stranami vpísaného uhla (obr. 332).
Nech ∠ABD je vpísaný uhol. Stred kruhu O leží medzi jeho stranami. Musíme dokázať, že ∠ABD sa meria polovicou oblúka AD.
Aby sme to dokázali, nakreslite priemer BC. Uhol ABD je rozdelený na dva uhly: ∠1 a ∠2.
∠1 sa meria polovicou oblúka AC a ∠2 sa meria polovicou oblúka CD, preto sa celé ∠ABD meria ako 1/2 \(\breve(AC)\) + 1/2 \(\breve (CD)\), t.j. polovičný oblúk AD.
Napríklad, ak \(\breve(AD)\) obsahuje 124°, potom ∠B obsahuje 62°.

Tretí prípad. Stred kružnice leží mimo vpísaného uhla (obr. 333).
Nech ∠MAD je vpísaný uhol. Stred kruhu O je mimo rohu. Musíme dokázať, že ∠MAD sa meria polovicou oblúka MD.
Aby sme to dokázali, nakreslíme priemer AB. ∠MAD = ∠MAB - ∠DAB. Ale ∠MAB meria 1/2 \(\breve(MB)\) a ∠DAB meria 1/2 \(\breve(DB)\).
Preto ∠MAD meria 1/2 (\(\breve(MB) - \breve(DB))\), t.j. 1/2 \(\breve(MD)\).
Napríklad, ak \(\breve(MD)\) obsahuje 48° 38", potom ∠MAD obsahuje 24° 19' 8".
Dôsledky
1.
Všetky vpísané uhly zvierajúce rovnaký oblúk sú si navzájom rovné, pretože sú merané polovicou toho istého oblúka
(Obr. 334, a).

2. Vpísaný uhol zovretý priemerom je pravý uhol, pretože zviera polovicu kruhu. Polovica kruhu obsahuje 180 oblúkových stupňov, čo znamená, že uhol založený na priemere obsahuje 90 oblúkových stupňov (obr. 334, b).
V tomto článku vám poviem, ako vyriešiť problémy, ktoré používajú .
Najprv si ako obvykle pripomeňme definície a vety, ktoré potrebujete vedieť, aby ste úspešne vyriešili problémy v .
1.Vpísaný uhol je uhol, ktorého vrchol leží na kružnici a ktorého strany kružnicu pretínajú:
2.Stredový uhol je uhol, ktorého vrchol sa zhoduje so stredom kruhu:

Hodnota stupňa kruhového oblúka merané hodnotou stredový uhol ktorý na ňom spočíva.
V tomto prípade sa hodnota stupňa oblúka AC rovná hodnote uhla AOS.
3. Ak sú vpísané a stredové uhly založené na rovnakom oblúku, potom vpísaný uhol je polovičný ako stredový uhol:
 4. Všetky vpísané uhly, ktoré spočívajú na jednom oblúku, sú si navzájom rovné:
4. Všetky vpísané uhly, ktoré spočívajú na jednom oblúku, sú si navzájom rovné:

5. Vpísaný uhol zovretý priemerom je 90°:

Poďme vyriešiť niekoľko problémov.
1. Úloha B7 (č. 27887)
Nájdite hodnotu stredového uhla, ktorý spočíva na rovnakom oblúku:
Je zrejmé, že uhol AOC sa rovná 90°, preto sa uhol ABC rovná 45°
Odpoveď: 45°
2. Úloha B7 (č. 27888)
Nájdite veľkosť uhla ABC. Uveďte svoju odpoveď v stupňoch.
Je zrejmé, že uhol AOC je 270°, potom uhol ABC je 135°.
Odpoveď: 135°
3. Úloha B7 (č. 27890)
Nájdite hodnotu stupňa oblúka AC kružnice zovretej uhlom ABC. Svoju odpoveď uveďte v stupňoch.
Nájdite hodnotu stredového uhla, ktorý spočíva na oblúku AC:
Veľkosť uhla AOS je 45°, preto je miera oblúka AC 45°.
Odpoveď: 45°.
4. Úloha B7 (č. 27885)
Nájdite uhol ACB, ak vpísané uhly ADB a DAE spočívajú na kruhových oblúkoch, ktorých hodnoty stupňov sa rovnajú resp. Svoju odpoveď uveďte v stupňoch.
Uhol ADB spočíva na oblúku AB, preto sa hodnota stredového uhla AOB rovná 118°, preto sa uhol BDA rovná 59° a susedný uhol ADC sa rovná 180°-59° = 121° 
Podobne uhol DOE je 38° a zodpovedajúci vpísaný uhol DAE je 19°.
Zvážte trojuholník ADC:
Súčet uhlov trojuholníka je 180°.
Uhol ACB sa rovná 180°- (121°+19°)=40°
Odpoveď: 40°
5. Úloha B7 (č. 27872)
Strany štvoruholníka ABCD AB, BC, CD a AD tvoria oblúky opísanej kružnice, ktorých hodnoty stupňov sa rovnajú , , resp. Nájdite uhol B tohto štvoruholníka. Uveďte svoju odpoveď v stupňoch.
 Uhol B spočíva na oblúku ADC, ktorého hodnota sa rovná súčtu hodnôt oblúkov AD a CD, teda 71°+145°=216°
Uhol B spočíva na oblúku ADC, ktorého hodnota sa rovná súčtu hodnôt oblúkov AD a CD, teda 71°+145°=216°
Vpísaný uhol B sa rovná polovici veľkosti oblúka ADC, teda 108°
Odpoveď: 108°
6. Úloha B7 (č. 27873)
Body A, B, C, D umiestnené na kružnici rozdeľujú túto kružnicu na štyri oblúky AB, BC, CD a AD, ktorých stupne sú v pomere 4:2:3:6. Nájdite uhol A štvoruholníka ABCD. Uveďte svoju odpoveď v stupňoch.
(pozri nákres predchádzajúcej úlohy)
Keďže sme uviedli pomer veľkostí oblúkov, zavedieme jednotkový prvok x. Potom bude veľkosť každého oblúka vyjadrená nasledujúcim pomerom:
AB=4x, BC=2x, CD=3x, AD=6x. Všetky oblúky tvoria kruh, to znamená, že ich súčet je 360°.
4x+2x+3x+6x=360°, teda x=24°.
Uhol A je podporený oblúkmi BC a CD, ktoré majú spolu hodnotu 5x=120°.
Preto je uhol A 60°
Odpoveď: 60°
7. Úloha B7 (č. 27874)
Štvoruholník A B C D vpísaný do kruhu. Rohový ABC rovný , uhol CAD
Dnes sa pozrieme na iný typ úloh 6 – tentoraz s kruhom. Mnohí študenti ich nemajú radi a považujú ich za ťažké. A úplne márne, pretože takéto problémy sú vyriešené elementárne, ak poznáte nejaké vety. Alebo sa vôbec neodvážia, ak ich nepoznáte.
Predtým, ako hovorím o hlavných vlastnostiach, dovoľte mi pripomenúť definíciu:
Vpísaný uhol je taký, ktorého vrchol leží na samotnom kruhu a ktorého strany vyrezávajú tetivu na tomto kruhu.
Stredový uhol je akýkoľvek uhol s vrcholom v strede kruhu. Jeho strany tiež pretínajú tento kruh a vyrezávajú na ňom tetivu.
Takže pojmy vpísaných a stredových uhlov sú neoddeliteľne spojené s kruhom a tetivami v ňom. A teraz hlavné vyhlásenie:
Veta. Stredový uhol je vždy dvojnásobkom vpísaného uhla na základe toho istého oblúka.
Napriek jednoduchosti výroku existuje celá trieda problémov 6, ktoré je možné pomocou neho vyriešiť – a nič iné.
Úloha. Nájdite ostrý vpísaný uhol zovretý tetivou, ktorá sa rovná polomeru kružnice.
Nech AB je tetiva, o ktorej uvažujeme, ó stred kruhu. Doplnková konštrukcia: OA a OB sú polomery kružnice. Dostaneme:

Zvážte trojuholník ABO. V ňom AB = OA = OB - všetky strany sa rovnajú polomeru kruhu. Preto je trojuholník ABO rovnostranný a všetky uhly v ňom sú 60°.
Nech M je vrchol vpísaného uhla. Pretože uhly O a M spočívajú na rovnakom oblúku AB, vpísaný uhol M je 2-krát menší ako stredový uhol O. Máme:
M = 0:2 = 60:2 = 30
Úloha. Stredový uhol je o 36° väčší ako vpísaný uhol zvieraný rovnakým oblúkom kružnice. Nájdite vpísaný uhol.
Predstavme si nasledujúci zápis:
- AB je tetiva kruhu;
- Bod O je stredom kruhu, takže uhol AOB je stredový uhol;
- Bod C je vrcholom vpísaného uhla ACB.

Keďže hľadáme vpísaný uhol ACB, označme ho ACB = x. Potom je stredový uhol AOB x + 36. Na druhej strane je stredový uhol 2-násobkom vpísaného uhla. Máme:
AOB = 2 · ACB;
x + 36 = 2 x;
x = 36.
Tak sme našli vpísaný uhol AOB - rovná sa 36°.
Kruh je uhol 360°
Po prečítaní podnadpisu si znalí čitatelia pravdepodobne teraz povedia: „Fuj!“ Naozaj, porovnávanie kruhu s uhlom nie je úplne správne. Aby ste pochopili, o čom hovoríme, pozrite sa na klasický trigonometrický kruh:

Na čo je tento obrázok? A okrem toho, plné otočenie je uhol 360 stupňov. A ak to rozdelíte, povedzme, na 20 rovnakých častí, potom veľkosť každej z nich bude 360: 20 = 18 stupňov. To je presne to, čo je potrebné na vyriešenie problému B8.
Body A, B a C ležia na kružnici a rozdeľte ju na tri oblúky, ktorých miera stupňov je v pomere 1 : 3 : 5. Nájdite väčší uhol trojuholníka ABC.
Najprv nájdime mieru každého oblúka. Menšia nech je x. Na obrázku je tento oblúk označený AB. Potom zostávajúce oblúky - BC a AC - môžu byť vyjadrené pomocou AB: oblúk BC = 3x; AC = 5x. Celkovo tieto oblúky dávajú 360 stupňov:
AB + BC + AC = 360;
x + 3x + 5x = 360;
9x = 360;
x = 40.
Teraz zvážte veľký oblúk AC, ktorý neobsahuje bod B. Tento oblúk, rovnako ako zodpovedajúci stredový uhol AOC, je 5x = 5 40 = 200 stupňov.
Uhol ABC je najväčší zo všetkých uhlov v trojuholníku. Je to vpísaný uhol zovretý rovnakým oblúkom ako stredový uhol AOC. To znamená, že uhol ABC je 2-krát menší ako AOC. Máme:
ABC = AOC: 2 = 200: 2 = 100
Toto bude miera väčšieho uhla v trojuholníku ABC.
Kružnica opísaná okolo pravouhlého trojuholníka
Mnoho ľudí zabúda na túto vetu. Ale márne, pretože niektoré problémy B8 sa bez toho nedajú vôbec vyriešiť. Presnejšie povedané, sú vyriešené, no s takým objemom výpočtov, že by ste radšej zaspali, ako by ste sa dopracovali k odpovedi.
Veta. Stred opísanej kružnice správny trojuholník, leží v strede prepony.
Čo z tejto vety vyplýva?
- Stred prepony je rovnako vzdialený od všetkých vrcholov trojuholníka. Toto je priamy dôsledok vety;
- Medián nakreslený k prepone rozdeľuje pôvodný trojuholník na dva rovnoramenné trojuholníky. To je presne to, čo je potrebné na vyriešenie problému B8.
V trojuholníku ABC nakreslíme stred CD. Uhol C je 90° a uhol B je 60°. Nájdite uhol ACD.
Pretože uhol C je 90°, trojuholník ABC je pravouhlý trojuholník. Ukazuje sa, že CD je medián k prepone. To znamená, že trojuholníky ADC a BDC sú rovnoramenné.
Zvážte najmä trojuholník ADC. V tom AD = CD. Ale v rovnoramennom trojuholníku sú uhly v základni rovnaké - pozri „Problém B8: Úsečky a uhly v trojuholníkoch“. Preto požadovaný uhol ACD = A.
Zostáva teda zistiť prečo rovný uhlu A. Aby sme to urobili, vráťme sa opäť k pôvodnému trojuholníku ABC. Označme uhol A = x. Keďže súčet uhlov v akomkoľvek trojuholníku je 180°, máme:
A + B + BCA = 180;
x + 60 + 90 = 180;
x = 30.
Samozrejme, posledný problém sa dá vyriešiť inak. Napríklad je ľahké dokázať, že trojuholník BCD nie je len rovnoramenný, ale rovnostranný. Takže uhol BCD je 60 stupňov. Uhol ACD je teda 90 − 60 = 30 stupňov. Ako vidíte, môžete použiť rôzne rovnoramenné trojuholníky, ale odpoveď bude vždy rovnaká.
Inštrukcie
Ak je známy polomer (R) kružnice a dĺžka oblúka (L) zodpovedajúca požadovanému stredovému uhlu (θ), možno ho vypočítať v stupňoch aj v radiánoch. Súčet je určený vzorcom 2*π*R a zodpovedá stredovému uhlu 360° alebo dvom číslam Pi, ak sa namiesto stupňov použijú radiány. Preto postupujte z podielu 2*π*R/L = 360°/θ = 2*π/θ. Vyjadrite z neho stredový uhol v radiánoch θ = 2*π/(2*π*R/L) = L/R alebo stupňov θ = 360°/(2*π*R/L) = 180*L/(π * R) a vypočítajte pomocou výsledného vzorca.
Na základe dĺžky tetivy (m) spájajúcej body určujúce stredový uhol (θ) možno vypočítať aj jej hodnotu, ak je známy polomer (R) kružnice. Za týmto účelom zvážte trojuholník tvorený dvoma polomermi a . Toto je rovnoramenný trojuholník, každý je známy, ale musíte nájsť uhol oproti základni. Sínus jeho polovice sa rovná pomeru dĺžky základne – tetivy – k dvojnásobku dĺžky strany – polomeru. Preto na výpočty použite funkciu inverzného sínusu - arcsine: θ = 2*arcsin(½*m/R).
Stredový uhol môže byť špecifikovaný v zlomkoch otáčky alebo od natočeného uhla. Napríklad, ak potrebujete nájsť stredový uhol zodpovedajúci štvrtine plný obrat, vydeľte 360° štyrmi: θ = 360°/4 = 90°. Rovnaká hodnota v radiánoch by mala byť 2*π/4 ≈ 3,14/2 ≈ 1,57. Rozvinutý uhol sa rovná polovici celej otáčky, preto napríklad stredový uhol zodpovedajúci jeho štvrtine bude mať polovicu hodnôt vypočítaných vyššie v stupňoch aj v radiánoch.
Inverzia sínusu sa nazýva goniometrická funkcia arkzín. Môže nadobudnúť hodnoty v rámci polovice Pi, kladné aj záporné pri meraní v radiánoch. Pri meraní v stupňoch budú tieto hodnoty v rozsahu od -90° do +90°.
Inštrukcie
Niektoré „okrúhle“ hodnoty sa nemusia počítať, ľahšie sa zapamätajú. Napríklad:- ak argument funkcie rovná nule, potom je jeho arcsínus tiež nula - od 1/2 sa rovná 30° alebo 1/6 Pi, ak sa meria - arkussínus -1/2 sa rovná -30° alebo -1/; 6 čísla Pi in - arkussínus od 1 sa rovná 90° alebo 1/2 Pi v radiánoch - arkussínus -1 sa rovná -90° alebo -1/2 Pi v radiánoch;
Na meranie hodnôt tejto funkcie z iných argumentov je najjednoduchšie použiť štandardnú kalkulačku Windows, ak ju máte po ruke. Ak chcete začať, otvorte hlavnú ponuku na tlačidle „Štart“ (alebo stlačením klávesu WIN), prejdite do časti „Všetky programy“ a potom do podsekcie „Príslušenstvo“ a kliknite na „Kalkulačka“.
Prepnite rozhranie kalkulačky do prevádzkového režimu, ktorý vám umožňuje počítať goniometrické funkcie. Ak to chcete urobiť, otvorte v jej ponuke sekciu „Zobraziť“ a vyberte „Inžinierstvo“ alebo „Vedecké“ (v závislosti od použitého operačného systému).
Zadajte hodnotu argumentu, z ktorého sa má vypočítať arkustangens. Môžete to urobiť kliknutím na tlačidlá na rozhraní kalkulačky pomocou myši alebo stlačením kláves na , alebo skopírovaním hodnoty (CTRL + C) a jej vložením (CTRL + V) do vstupného poľa kalkulačky.
Vyberte jednotky merania, v ktorých potrebujete získať výsledok výpočtu funkcie. Pod vstupným poľom sú tri možnosti, z ktorých je potrebné vybrať (kliknutím myšou) jednu - , radiány alebo rads.
Začiarknite políčko, ktoré invertuje funkcie zobrazené na tlačidlách rozhrania kalkulačky. Stojí vedľa neho krátky nápis Inv.
Kliknite na tlačidlo hriechu. Kalkulačka prevráti funkciu s ňou spojenú, vykoná výpočet a predloží vám výsledok v zadaných jednotkách.
Video k téme
Jedným z bežných geometrických problémov je výpočet plochy kruhového segmentu - časť kruhu ohraničená tetivou a zodpovedajúca tetiva oblúkom kruhu.

Plocha kruhového segmentu sa rovná rozdielu medzi plochou príslušného kruhového sektora a plochou trojuholníka tvoreného polomermi sektora zodpovedajúcimi segmentu a tetivou obmedzujúcou segment.
Príklad 1
Dĺžka tetivy pretínajúcej kružnicu sa rovná hodnote a. Miera stupňa oblúka zodpovedajúceho tetive je 60°. Nájdite oblasť kruhového segmentu.
Riešenie
Trojuholník tvorený dvoma polomermi a tetivou je rovnoramenný, takže nadmorská výška nakreslená od vrcholu stredového uhla k strane trojuholníka tvoreného tetivou bude tiež osou stredového uhla, ktorá ho rozdelí na polovicu a medián, deliaci akord na polovicu. S vedomím, že sínus uhla sa rovná pomeru opačnej nohy k prepone, môžeme vypočítať polomer:
Sin 30°= a/2:R = 1/2;
Sc = πR2/360°*60° = πa2/6
Plocha trojuholníka zodpovedajúca sektoru sa vypočíta takto:
S▲=1/2*ah, kde h je výška vedená od vrcholu stredového uhla k tetive. Podľa Pytagorovej vety h=√(R²-a²/4)= √3*a/2.
V súlade s tým S▲=√3/4*a².
Plocha segmentu, vypočítaná ako Sreg = Sc - S▲, sa rovná:
Sreg = πa²/6 - √3/4*a²
Nahradením číselnej hodnoty za hodnotu a môžete jednoducho vypočítať číselnú hodnotu oblasti segmentu.
Príklad 2
Polomer kruhu sa rovná a. Miera stupňa oblúka zodpovedajúceho segmentu je 60°. Nájdite oblasť kruhového segmentu.
Riešenie:
Plochu sektora zodpovedajúcu danému uhlu možno vypočítať pomocou nasledujúceho vzorca:
Proces prípravy na jednotnú štátnu skúšku z matematiky sa najčastejšie začína opakovaním základných definícií, vzorcov a teorémov, a to aj na tému „Stredové a vpísané uhly v kruhu“. Spravidla sa tento úsek planimetrie študuje v stredná škola. Nie je prekvapujúce, že mnohí študenti čelia potrebe zopakovať si základné pojmy a vety na tému „Stredný uhol kruhu“. Po pochopení algoritmu na riešenie takýchto problémov môžu školáci počítať s tým, že získajú konkurenčné skóre na základe výsledkov zloženia jednotnej štátnej skúšky.
Ako sa jednoducho a efektívne pripraviť na absolvovanie certifikačného testu?
Pri štúdiu pred zložením jednotnej štátnej skúšky sa mnohí stredoškoláci stretávajú s problémom nájsť potrebné informácie na tému „Stredové a vpísané uhly v kruhu“. Nie vždy je po ruke školská učebnica. A hľadanie vzorcov na internete niekedy zaberie veľa času.
Náš tím vám pomôže „napumpovať“ vaše schopnosti a zlepšiť vaše znalosti v takej náročnej sekcii geometrie, akou je planimetria vzdelávací portál. „Shkolkovo“ ponúka študentom stredných škôl a ich učiteľom nový spôsob, ako vybudovať proces prípravy na jednotnú štátnu skúšku. Všetok základný materiál je prezentovaný našimi špecialistami v najdostupnejšej forme. Po prečítaní informácií v časti „Teoretické východiská“ sa študenti dozvedia, aké vlastnosti má stredový uhol kruhu, ako zistiť jeho hodnotu atď.
Potom na upevnenie získaných vedomostí a cvičných zručností odporúčame vykonať vhodné cvičenia. Veľký výber úloh na zistenie veľkosti uhla vpísaného do kruhu a ďalších parametrov je uvedený v časti „Katalóg“. Pre každé cvičenie naši odborníci napísali podrobné riešenie a označili správnu odpoveď. Zoznam úloh na stránke sa neustále dopĺňa a aktualizuje.
Stredoškoláci sa môžu pripraviť na Jednotnú štátnu skúšku precvičovaním cvičení, napríklad na zistenie veľkosti stredového uhla a dĺžky kruhového oblúka, online z akéhokoľvek ruského regiónu.
Dokončenú úlohu je možné v prípade potreby uložiť do časti „Obľúbené“, aby ste sa k nej mohli neskôr vrátiť a ešte raz analyzovať princíp jej riešenia.