Somme de tous les angles d'un triangle. Somme des angles d'un triangle. Cours complets – Hypermarché du savoir

Le fait que « la somme des angles de tout triangle dans la géométrie euclidienne est de 180 degrés » peut simplement être rappelé. Si ce n’est pas facile à retenir, vous pouvez réaliser quelques expériences pour une meilleure mémorisation.

Première expérience

Dessinez plusieurs triangles arbitraires sur une feuille de papier, par exemple :

• avec des côtés arbitraires ;
• triangle isocèle;
• triangle rectangle.

Assurez-vous d'utiliser une règle. Vous devez maintenant découper les triangles résultants, en le faisant exactement le long des lignes tracées. Coloriez les coins de chaque triangle avec un crayon de couleur ou un marqueur. Par exemple, dans le premier triangle, tous les coins seront rouges, dans le deuxième, bleus, dans le troisième, verts. http://bit.ly/2gY4Yfz

À partir du premier triangle, coupez les 3 coins et reliez-les en un point avec leurs sommets, de sorte que les côtés les plus proches de chaque coin soient connectés. Comme vous pouvez le voir, les trois coins du triangle formaient un angle étendu égal à 180 degrés. Faites de même avec les deux autres triangles – le résultat sera le même. http://bit.ly/2zurCrd

Deuxième expérience

Dessinez un triangle arbitraire ABC. Nous sélectionnons n'importe quel sommet (par exemple, C) et traçons une ligne droite DE qui le traverse, parallèle au côté opposé (AB). http://bit.ly/2zbYNzq

Nous obtenons ce qui suit :

1. Les angles BAC et ACD sont égaux aux angles internes perpendiculaires à AC ;
2. Les angles ABC et BCE sont égaux aux angles internes perpendiculaires à BC ;
3. On voit que les angles 1, 2 et 3 sont les angles d'un triangle, reliés en un point pour former un angle développé DCE, qui est égal à 180 degrés.

Le théorème de la somme des angles du triangle stipule que la somme de tous les angles intérieurs d’un triangle est de 180°.

Soient les angles intérieurs d'un triangle a, b et c, alors :

a + b + c = 180°.

De cette théorie, nous pouvons conclure que la somme de tous les angles externes de tout triangle est égale à 360°. Puisqu’un angle externe est adjacent à un angle interne, leur somme est de 180°. Soit les angles intérieurs d'un triangle a, b et c, alors les angles extérieurs à ces angles sont 180° - a, 180° - b et 180° - c.

Trouvons la somme des angles externes d'un triangle :

180° - a + 180° - b + 180° - c = 540° - (a + b + c) = 540° - 180° = 360°.

Réponse : la somme des angles intérieurs d’un triangle est de 180° ; la somme des angles extérieurs d'un triangle est de 360°.

Ce théorème est également formulé dans le manuel de L.S. Atanasyan. , et dans le manuel de Pogorelov A.V. . Les preuves de ce théorème dans ces manuels ne diffèrent pas de manière significative, et c'est pourquoi nous présentons sa preuve, par exemple, du manuel d'A.V. Pogorelov.

Théorème : La somme des angles d'un triangle est 180°

Preuve. Soit ABC le triangle donné. Traçons une ligne passant par le sommet B parallèle à la ligne AC. Marquons dessus le point D de manière à ce que les points A et D se trouvent le long différents côtés de la ligne directe BC (Fig. 6).

Les angles DBC et ACB sont égaux aux angles internes croisés, formés par la sécante BC avec les droites parallèles AC et BD. Par conséquent, la somme des angles d’un triangle aux sommets B et C est égale à l’angle ABD. Et la somme des trois angles d’un triangle est égale à la somme des angles ABD et BAC. Puisqu’il s’agit d’angles intérieurs unilatéraux pour les parallèles AC et BD et sécants AB, leur somme est de 180°. Le théorème est prouvé.

L'idée de cette preuve est de tracer une ligne parallèle et d'indiquer que les angles requis sont égaux. Reconstruisons l'idée d'une telle construction supplémentaire en prouvant ce théorème en utilisant le concept d'expérience de pensée. Preuve du théorème à l'aide d'une expérience de pensée. Ainsi, le sujet de notre expérience de pensée concerne les angles d’un triangle. Plaçons-le mentalement dans des conditions où son essence peut se révéler avec une certitude particulière (étape 1).

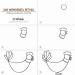
De telles conditions seront une telle disposition des coins du triangle dans laquelle leurs trois sommets seront combinés en un seul point. Une telle combinaison est possible si l'on autorise la possibilité de « déplacer » les coins en déplaçant les côtés du triangle sans changer l'angle d'inclinaison (Fig. 1). De tels mouvements sont essentiellement des transformations mentales ultérieures (étape 2).

En désignant les angles et les côtés d'un triangle (Fig. 2), les angles obtenus en « bougeant », nous formons ainsi mentalement l'environnement, le système de connexions dans lequel nous plaçons notre sujet de pensée (étape 3).

La ligne AB, « se déplaçant » le long de la ligne BC et sans changer l'angle d'inclinaison, transfère l'angle 1 à l'angle 5, et « se déplaçant » le long de la ligne AC, transfère l'angle 2 à l'angle 4. Puisqu'avec un tel « mouvement » la ligne AB ne change pas l'angle d'inclinaison des lignes AC et BC, alors la conclusion est évidente : les rayons a et a1 sont parallèles à AB et se transforment l'un dans l'autre, et les rayons b et b1 sont respectivement une continuation des côtés BC et AC. Puisque l’angle 3 et l’angle entre les rayons b et b1 sont verticaux, ils sont égaux. La somme de ces angles est égale à l’angle de rotation aa1, soit 180°.

CONCLUSION

DANS travail de diplôme des preuves « construites » de certains théorèmes géométriques scolaires ont été réalisées en utilisant la structure d'une expérience de pensée, qui a confirmé l'hypothèse formulée.

Les preuves présentées étaient basées sur de telles idéalisations visuelles et sensorielles : « compression », « étirement », « glissement », qui ont permis de transformer l'objet géométrique original d'une manière particulière et de mettre en évidence ses caractéristiques essentielles, typiques d'une pensée. expérience. Dans ce cas, une expérience de pensée agit comme un certain « outil créatif » qui contribue à l'émergence de connaissances géométriques (par exemple, sur ligne médiane trapèze ou autour des angles d'un triangle). De telles idéalisations permettent d'appréhender toute l'idée de preuve, l'idée de réaliser une « construction supplémentaire », ce qui permet de parler de la possibilité d'une compréhension plus consciente par les écoliers du processus de preuve déductive formelle de théorèmes géométriques.

Une expérience de pensée est l'une des méthodes de base obtenir et découvrir des théorèmes géométriques. Il est nécessaire de développer une méthodologie pour transférer la méthode à l'étudiant. Restes question ouverte sur l'âge d'un élève acceptable pour « accepter » la méthode, sur « Effets secondaires» les preuves ainsi présentées.

Ces questions nécessitent une étude plus approfondie. Mais en tout cas, une chose est sûre : une expérience de pensée se développe chez les écoliers pensée théorique, constitue sa base et, par conséquent, la capacité d’expérimentation mentale doit être développée.

>>Géométrie : Somme des angles d'un triangle. Cours complets

SUJET DE LA LEÇON : Somme des angles d'un triangle.

Objectifs de la leçon:

• Consolider et tester les connaissances des étudiants sur le thème : « Somme des angles d'un triangle » ;
• Preuve des propriétés des angles d'un triangle ;
• Application de cette propriété à la résolution de problèmes simples ;
• Utiliser du matériel historique pour développer l’activité cognitive des élèves ;
• Inculquer la compétence de précision lors de la construction de dessins.

Objectifs de la leçon:

• Testez les compétences des élèves en résolution de problèmes.

Plan de cours:

1. Triangle;
2. Théorème sur la somme des angles d'un triangle ;
3. Exemples de tâches.

Triangle.

Fichier:O.gif Triangle- le polygone le plus simple ayant 3 sommets (angles) et 3 côtés ; partie du plan délimitée par trois points et trois segments reliant ces points deux à deux.
Trois points de l'espace qui ne se trouvent pas sur la même droite correspondent à un et un seul plan.
N'importe quel polygone peut être divisé en triangles - ce processus est appelé triangulation.
Il existe une section de mathématiques entièrement consacrée à l'étude des lois des triangles - Trigonométrie.

Théorème sur la somme des angles d'un triangle.

Fichier:T.gif Le théorème de la somme des angles du triangle est un théorème classique de la géométrie euclidienne qui stipule que la somme des angles d'un triangle est de 180°.

Preuve" :

Soit Δ ABC. Traçons une ligne parallèle à (AC) passant par le sommet B et marquons dessus le point D de sorte que les points A et D se trouvent sur les côtés opposés de la ligne BC. Alors l'angle (DBC) et l'angle (ACB) sont égaux comme étant internes transversalement aux droites parallèles BD et AC et à la sécante (BC). Alors la somme des angles du triangle aux sommets B et C est égale à l'angle (ABD). Mais l'angle (ABD) et l'angle (BAC) au sommet A du triangle ABC sont unilatéraux internes aux droites parallèles BD et AC et à la sécante (AB), et leur somme est de 180°. La somme des angles d’un triangle vaut donc 180°. Le théorème est prouvé.

Conséquences.

Angle externe d'un triangle égal à la somme deux angles d'un triangle qui ne lui sont pas adjacents.

Preuve:

Soit Δ ABC. Le point D se trouve sur la droite AC de sorte que A se situe entre C et D. Alors BAD est extérieur à l'angle du triangle au sommet A et A + BAD = 180°. Mais A + B + C = 180°, et donc B + C = 180° – A. Donc BAD = B + C. Le corollaire est prouvé.

Conséquences.

L’angle extérieur d’un triangle est plus grand que tout angle du triangle qui ne lui est pas adjacent.

Tâche.

Un angle extérieur d'un triangle est un angle adjacent à n'importe quel angle de ce triangle. Montrer que l'angle extérieur d'un triangle est égal à la somme de deux angles du triangle qui ne lui sont pas adjacents.
(Fig. 1)

Solution:

Soit Δ ABC ∠DAС externe (Fig. 1). Alors ∠DAC=180°-∠BAC (par propriété coins adjacents), d'après le théorème sur la somme des angles d'un triangle ∠B+∠C = 180°-∠BAC. De ces égalités on obtient ∠DAС=∠В+∠С

Fait intéressant:

Somme des angles d'un triangle" :

En géométrie Lobatchevski, la somme des angles d'un triangle est toujours inférieure à 180. En géométrie euclidienne, elle est toujours égale à 180. En géométrie Riemann, la somme des angles d'un triangle est toujours supérieure à 180.

De l'histoire des mathématiques :

Euclide (IIIe siècle avant JC) dans son ouvrage « Éléments » donne la définition suivante : « Les lignes parallèles sont des lignes qui sont dans le même plan et, s'étendant indéfiniment dans les deux directions, ne se rencontrent d'aucun côté. »
Posidonius (1er siècle avant JC) « Deux lignes droites situées dans le même plan, également espacées l'une de l'autre »
L'ancien scientifique grec Pappus (IIIe siècle avant JC) a introduit le symbole des lignes parallèles - le signe =. Par la suite, l’économiste anglais Ricardo (1720-1823) utilisa ce symbole comme signe égal.
Ce n'est qu'au XVIIIe siècle qu'ils ont commencé à utiliser le symbole des lignes parallèles - le signe ||.
Le lien vivant entre les générations n'est pas interrompu un instant ; chaque jour, nous apprenons l'expérience accumulée par nos ancêtres. Les anciens Grecs, sur la base d'observations et d'expériences pratiques, tiraient des conclusions, exprimaient des hypothèses, puis, lors de réunions de scientifiques - des colloques (littéralement « festin ») - ils essayaient de justifier et de prouver ces hypothèses. À cette époque, la déclaration est apparue : « La vérité naît dans la contestation ».

Des questions:

1. Qu'est-ce qu'un triangle ?
2. Que dit le théorème sur la somme des angles d’un triangle ?
3. Quel est l'angle extérieur du triangle ?

Buts et objectifs:

Éducatif:

• répéter et généraliser les connaissances sur le triangle ;
• prouver le théorème sur la somme des angles d'un triangle ;
• vérifier pratiquement l'exactitude de la formulation du théorème ;
• apprendre à appliquer les connaissances acquises lors de la résolution de problèmes.

Éducatif:

• développer la pensée géométrique, l'intérêt pour le sujet, les fonctions cognitives et activité créativeétudiants, discours mathématique, capacité d'acquérir des connaissances de manière indépendante.

Éducatif:

• développer qualités personnellesétudiants, comme la détermination, la persévérance, la précision, la capacité à travailler en équipe.

Équipement: projecteur multimédia, triangles en papier de couleur, complexe pédagogique « Mathématiques vivantes », ordinateur, écran.

Étape préparatoire : L'enseignant donne à l'élève la tâche de se préparer information historiqueà propos du théorème « Somme des angles d’un triangle ».

Type de cours: apprendre du nouveau matériel.

Pendant les cours

I. Moment organisationnel

Salutations. Attitude psychologique des étudiants envers le travail.

II. Réchauffer

AVEC figure géométrique« triangle » que nous avons rencontré dans les leçons précédentes. Répétons ce que l'on sait du triangle ?

Les étudiants travaillent en groupes. Ils ont la possibilité de communiquer entre eux, chacun construisant indépendamment le processus cognitif.

Ce qui s'est passé? Chaque groupe fait ses propositions, l'enseignant les écrit au tableau. Les résultats sont discutés :

Image 1

III. Formuler l'objectif de la leçon

Nous en savons donc déjà beaucoup sur le triangle. Mais pas tout. Chacun de vous a des triangles et des rapporteurs sur son bureau. Quel genre de problème pensez-vous que nous pouvons formuler ?

Les élèves formulent la tâche de la leçon : trouver la somme des angles d'un triangle.

IV. Explication du nouveau matériel

Partie pratique(favorise la mise à jour des connaissances et des compétences de connaissance de soi). Mesurez les angles à l'aide d'un rapporteur et trouvez leur somme. Notez les résultats dans votre cahier (écoutez les réponses reçues). On découvre que la somme des angles est différente pour chacun (cela peut arriver parce que le rapporteur n'a pas été appliqué avec précision, que le calcul a été effectué avec négligence, etc.).

Effectuer les virages selon pointillés et découvrez à quoi d'autre la somme des angles d'un triangle est égale :

UN)
Figure 2

b)
figure 3

V)
Figure 4

G)
Figure 5

d)
Figure 6

Après avoir réalisé les travaux pratiques, les étudiants formulent la réponse : La somme des angles d'un triangle est égale au degré de l'angle déplié, soit 180°.

Enseignant : En mathématiques Travaux pratiques Cela permet seulement de faire une sorte de déclaration, mais cela doit être prouvé. Un énoncé dont la validité est établie par une preuve s'appelle un théorème. Quel théorème pouvons-nous formuler et prouver ?

Étudiants: La somme des angles d'un triangle est de 180 degrés.

Référence historique : La propriété de la somme des angles d'un triangle a été établie dans L'Egypte ancienne. La preuve, exposée dans les manuels modernes, est contenue dans le commentaire de Proclus sur les Éléments d'Euclide. Proclus prétend que cette preuve (Fig. 8) a été découverte par les Pythagoriciens (Ve siècle avant JC). Dans le premier livre des Éléments, Euclide expose une autre preuve du théorème sur la somme des angles d'un triangle, facile à comprendre à l'aide d'un dessin (Fig. 7) :

Figure 7

Figure 8

Les dessins sont affichés sur l'écran grâce à un projecteur.

L'enseignant propose de prouver le théorème à l'aide de dessins.

Ensuite, la preuve est réalisée à l'aide du complexe d'enseignement et d'apprentissage « Mathématiques vivantes ». L'enseignant projette la preuve du théorème sur l'ordinateur.

Théorème sur la somme des angles d'un triangle : "La somme des angles d'un triangle est 180°"

Figure 9

Preuve:

UN)

Figure 10

b)

Figure 11

V)

Figure 12

Les élèves notent brièvement la preuve du théorème dans leur cahier :

Théorème: La somme des angles d'un triangle est de 180°.

Figure 13

Donné:ΔABC

Prouver: A + B + C = 180°.

Preuve:

Ce qu’il fallait prouver.

V. Phys. juste une minute.

VI. Explication du nouveau matériel (suite)

Le corollaire du théorème sur la somme des angles d'un triangle est déduit par les élèves de manière indépendante, cela contribue au développement de la capacité à formuler son propre point de vue, à l'exprimer et à l'argumenter :

Dans n'importe quel triangle, soit tous les angles sont aigus, soit deux angles aigus, et le troisième est obtus ou droit.

Si un triangle a tous des angles aigus, alors on l'appelle à angle aigu.

Si l’un des angles d’un triangle est obtus, alors on l’appelle à angle obtus.

Si l’un des angles d’un triangle est droit, alors on l’appelle rectangulaire.

Le théorème sur la somme des angles d'un triangle permet de classer les triangles non seulement par côtés, mais aussi par angles. (Au fur et à mesure que les élèves présentent les types de triangles, les élèves remplissent le tableau)

Tableau 1

Vue triangulaire	Isocèle	Équilatéral	Polyvalent
Rectangulaire
Obtus
Angle aigu

VII. Consolidation du matériel étudié.

1. Résoudre les problèmes oralement :

(Les dessins sont affichés sur l'écran via un projecteur)

Tâche 1. Trouver l'angle C.

Figure 14

Problème 2. Trouvez l'angle F.

Figure 15

Tâche 3. Trouvez les angles K et N.

Figure 16

Problème 4. Trouvez les angles P et T.

Figure 17

1. Résolvez vous-même le problème n° 223 (b, d).
2. Résoudre le problème au tableau et dans les cahiers, élève n°224.
3. Questions : Un triangle peut-il avoir : a) deux angles droits ; b) deux angles obtus ; c) un angle droit et un angle obtus.
4. (fait oralement) Les cartes sur chaque table montrent différents triangles. Déterminez à l’œil nu le type de chaque triangle.

Figure 18

1. Trouvez la somme des angles 1, 2 et 3.

Figure 19

VIII. Résumé de la leçon.

Enseignant : Qu'avons-nous appris ? Le théorème est-il applicable à n’importe quel triangle ?

IX. Réflexion.

Dites-moi votre humeur, les gars ! AVEC verso utilisez un triangle pour représenter vos expressions faciales.

Figure 20

Devoirs: paragraphe 30 (partie 1), question 1 ch. IV page 89 du manuel ; N° 223 (a, c), n° 225.

"Dis-moi et j'oublierai,
Montre-moi et je me souviendrai
Impliquez-moi et j’apprendrai”
Proverbe oriental

Objectif : prouver le théorème sur la somme des angles d'un triangle, s'entraîner à résoudre des problèmes en utilisant ce théorème, développer l'activité cognitive des élèves en utilisant du matériel supplémentaire provenant de différentes sources et développer la capacité d'écouter les autres.

Équipement: Rapporteur, règle, modèles triangulaires, bande d'humeur.

PENDANT LES COURS

1. Moment organisationnel.

Marquez votre humeur au début de la leçon sur la bande d'humeur.

2. Répétition.

Revoyez les concepts qui seront utilisés pour prouver le théorème : propriétés des angles pour les droites parallèles, définition d'un angle droit, mesure en degrés d'un angle droit.

3. Nouveau matériel.

3.1. Travaux pratiques.

Chaque élève dispose de trois modèles de triangle : aigu, rectangulaire et obtus. Il est proposé de mesurer les angles d'un triangle et de trouver leur somme. Analysez le résultat. Vous pouvez obtenir des valeurs de 177, 178, 179, 180, 181, 182, 183 degrés. Calculez la moyenne arithmétique (=180°). Il est suggéré de se rappeler quand les angles ont une mesure en degrés de 180 degrés. Les élèves se souviennent qu’il s’agit d’un angle droit et de la somme d’angles unilatéraux.

Essayons d'obtenir la somme des angles d'un triangle en utilisant l'origami.

Référence historique

L'origami (en japonais, lit. : « papier plié ») est l'art ancien du pliage de figurines en papier. L’art de l’origami trouve ses racines dans la Chine ancienne, où le papier a été découvert.

3.2. Preuve du théorème du manuel d'Atanasyan L.S.

Théorème sur la somme des angles d'un triangle.

Démontrons l'un des théorèmes de géométrie les plus importants - le théorème sur la somme des angles d'un triangle.

Théorème. La somme des angles d'un triangle est de 180°.

Preuve. Considérons un triangle arbitraire ABC et prouvez que A + B + C = 180°.

Traçons une droite a passant par le sommet B, parallèle au côté AC. Les angles 1 et 4 sont des angles croisés lorsque les lignes parallèles a et AC sont coupées par la sécante AB, et les angles 3 et 5 sont des angles croisés lorsque les mêmes lignes parallèles sont coupées par la sécante BC. L'angle est donc 4 égal à l'angle 1, l'angle 5 est égal à l'angle 3.

Évidemment, la somme des angles 4, 2 et 5 est égale à l'angle développé de sommet B, soit angle 4 + angle 2 + angle 5 = 180°. De là, en tenant compte des égalités précédentes, on obtient : angle 1 + angle 2+ angle 3 = 180°, soit A + B+ C = 180°. Le théorème est prouvé.

3.3. Preuve du théorème tirée du manuel de A. V. Pogorelov.

Prouver : A + B + C = 180°

Preuve:

1. Tracez une ligne BD // AC passant par le sommet B

2. DBC=ACB, couché transversalement à AC//BD et sécant BC.

3. ABD=ACB +CBD

Donc A + B + C = ABD + BAC

4. ABD et BAC sont unilatéraux avec BD // AC et AB sécants, ce qui signifie que leur somme est égale à 180°, soit A+B + C=180°, c'est ce qu'il fallait prouver.

3. 4. Preuve du théorème du manuel de Kiselev A.N., Rybkina N.A.

Donné: abc

Prouver: A+B +C=180°

Preuve:

1. Continuons le côté AC. Nous réaliserons CE//AV

2. A=ESD, correspondant à AB//CE et AD - sécant

3. B=ALL, situé transversalement à AB//CE et BC - la sécante.

4. ESD + ALL + C = 180°, ce qui veut dire A + B + C = 180°, ce qu'il fallait prouver.

3.5. Corollaires 1. Dans tout triangle, tous les angles sont aigus, ou deux angles sont aigus et le troisième est obtus ou droit.

Corollaire 2.

Un angle extérieur d’un triangle est égal à la somme des deux autres angles du triangle qui ne lui sont pas adjacents.

3.6. Le théorème nous permet de classer les triangles non seulement par côtés, mais aussi par angles.

Vue triangulaire	Isocèle	Équilatéral	Polyvalent
rectangulaire
obtus
à angle aigu

4. Consolidation.

4.1. Résoudre des problèmes à l'aide de dessins prêts à l'emploi.

Trouvez les angles inconnus du triangle.

4.2. Vérification des connaissances.

1. À la fin de notre leçon, répondez aux questions :

Existe-t-il des triangles avec des angles :

a) 30, 60, 90 degrés,

b) 46, 4, 140 degrés,

c) 56, 46, 72 degrés ?

2. Un triangle peut-il avoir :

a) deux angles obtus,

b) angles obtus et droits,

c) deux angles droits ?

3. Déterminez le type de triangle si un angle est de 45 degrés et l'autre de 90 degrés.

4. Dans quel triangle la somme des angles est-elle la plus grande : aigu, obtus ou rectangulaire ?

5. Est-il possible de mesurer les angles de n’importe quel triangle ?

C'est une question plaisante, parce que... Il existe un Triangle des Bermudes, situé dans l’océan Atlantique entre les Bermudes, l’État de Porto Rico et la péninsule de Floride, dont les angles ne peuvent être mesurés. (Annexe 1)

5. Résumé de la leçon.

Marquez votre humeur à la fin de la leçon sur la bande d'humeur.

Devoirs.

P. 30-31 ; N° 223 a, b ; n° 227a ; classeur № 116, 118.